古代玻璃制品的成分分析与鉴别
[TOC]
摘要
本文基于一批我国古代玻璃制品的相关数据进行了古代玻璃制品的成分分析与鉴别,建立了古代玻璃制品鉴别模型,对各问题进行了分析。
对于问题一,针对玻璃文物的表面风化与玻璃类型、纹饰和颜色是否具有关系的问题,计算玻璃类型、颜色、纹饰与表面风化的斯皮尔曼系数,分析相关性,得到结论“表面风化和玻璃类型关系最大,和玻璃颜色与纹饰的关系不大”。为预测其风化前的化学成分含量,通过分析文物表面风化前后化学成分含量变化的统计学规律,结合聚类分析及多项式曲线拟合,对风化前数据进行了预测,预测详情数据见支撑材料。
对于问题二,首先,为得出高钾玻璃和铅钡玻璃的分类规律,将无风化的高钾和铅钡玻璃各化学成分含量的均值曲线进行对比,采用统计学方法分析得出高钾玻璃、铅钡玻璃的分类规律。其次,为解决高钾玻璃和铅钡玻璃的亚类划分问题,运用SPSS工具,采用聚类分析法,依据各样本每种化学成分含量与其他样本各化学成分含量之间的联系进行聚类。聚类完成后再加以统计学分析,寻找其聚为一类的原因并从中提炼分类特征。最终聚类结果为:高钾玻璃分3类,分别为低铅钡玻璃、高磷玻璃、高铜玻璃;铅钡玻璃分5类,分别为高磷玻璃、高钠玻璃、高铝玻璃、钙铁玻璃、高铜玻璃。之后通过计算轮廓系数分析得到模型的合理性,并通过增添样本衡量分类结果的敏感性。
对于问题三,在对附件表单3中未知类别玻璃文物的化学成分进行分析时先将数据分为无风化和风化,之后经由表单2按照风化、无风化的标准通过箱图、散点图进行数据分析找出适合做自变量的化学成分,确定自变量和因变量从而建立多元回归模型。通过SPSS并依据建立的模型确定影响较高的化学成分进而推测其所属类型。可知高钾玻璃分别是A1、A4、A6、A7,铅钡玻璃分别是A2、A3、A5、A8。在敏感性分析上,更改各项系数中的一项,取附录2中数据代入计算,原计算结果与新数据的变化很明显,数据显著性很强。
对于问题四,针对不同类别的玻璃文物样品,使用灰色关联分析法分析其化学成分之间的关联关系,得出不同种类的玻璃所含化学成分的关联系数并对其进行排序。通过对不同玻璃类型的数据进行灰色关联分析,得到几组不同的关系系数列表,通过各个关系系数列表的对比,体现不同种类玻璃化学成分关联关系的差异性。
关键词:多元回归 斯皮尔曼系数 聚类分析 灰色关联分析
一、问题重述
1.1问题背景
玻璃的出现与使用在人类的生活里已有四千多年的历史,早期的玻璃在西亚和埃及地区常被制作成珠形饰品。历史上古代玻璃经由丝绸之路传入我国,我国古代玻璃吸收其技术后在本土就地取材制作,因此与外来的玻璃制品外观相似,但化学成分却不相同。从西周到两汉时期中国境内玻璃制品化学成分的演变有自己独特的发展脉络,研究不同时期古代玻璃组成成分,对于了解古代金属冶炼技术与古代丝绸之路等有重大意义。
在长期的风化过程中,内部的各种氧化物与环境中的各种元素之间存在大量的物理和化学反应,一些组成元素的交换导致其组成比例的变化,这将影响对其类别的正确判断。
1.2 具体问题重述
现有一批我国古代玻璃制品的相关数据,考古工作者现已将其分为高钾玻璃和铅钡玻璃两种类型。
问题一:建立模型确定玻璃文物的表面风化与玻璃类型、纹饰和颜色是否具有关联关系,并根据玻璃类型分析文物表面风化前后化学成分含量变化的统计规律。根据风化点的检测数据,建立预测模型,预测该文物风化前各化学成分的所占比例。
问题二:由附件表单2中的数据分析高钾玻璃和铅钡玻璃的分类规则;对于每个类别,通过聚类分析选择合适的化学成分来划分其子类,给出具体的分类方法和划分结果,并分析划分结果的合理性和敏感性。
问题三:对附件表单 3 中未知类别玻璃文物的化学成分分析,鉴别其类型,并对分类结果的敏感性进行分析。
问题四:分析不同类型的玻璃样品化学组成之间的关联,比较不同类别玻璃文物样品之间关联关系的差异。
二、问题分析
2.1对问题一的分析
2.1.1表面风化与玻璃类型、纹饰和颜色的关系
分析表面风化与玻璃类型、纹饰和颜色的关系是经典的相关性分析,可以通过皮尔逊系数或斯皮尔曼系数分析相关性。皮尔逊系数进行关联性分析需要呈正态分布且是线性关系的连续变量,而玻璃类型、纹饰、颜色均为定类,而非定量故选择斯皮尔曼系数分析相关性。
2.1.2文物样品表面有无风化化学成分含量的统计规律
本文通过聚类分析,将14种不同变量进行聚类,并结合聚类结果,使用多项式曲线拟合,通过对不同指标的关系对风化前的化学成分利用构建的以小二乘法为思路的多元函数表达式进行求解。
经过数据处理后,可以发现高钾玻璃风化前后化学成分变化具有明显相关性,而铅钡玻璃则不具有明显相关性而无法使用多元线性回归模型求解。
继续通过多元线性回归模型预测高钾玻璃风化前数据,通过聚类结果并结合统计学规律预测铅钡玻璃风化前成分。
2.2对问题二的分析
要从化学成分含量角度分析高钾玻璃、铅钡玻璃的分类规律应建立在玻璃无风化、化学成分含量未被破坏的前提下,根据无风化状态下不同类型玻璃化学成分含量分布曲线,将无风化的高钾和铅钡玻璃各化学成分含量的均值曲线进行对比,分析得出高钾玻璃、铅钡玻璃的分类规律。
根据化学成分进行亚分类是一个聚类问题,事先并不知道要分为多少类,我们考虑使用系统聚类法,将各样本作为聚类对象,依据其每种化学成分含量与其他样本各化学成分含量之间的联系进行聚类。系统聚类完成后得出初步聚类结果,而后加以统计学分析,从化学成分含量的角度找出各聚类组合之所以聚为一类的原因,对于一些规律不很明显的组合适当进行人工干预重新组合,提炼出分类特征从而形成类标签,实现基于化学成分的亚类划分。之后通过计算轮廓系数分析得到模型的合理性,并通过增添测试数据衡量分类的敏感性。
2.3对问题三的分析
在判别玻璃文物类型前,先将数据划分为无风化的未知类别玻璃文物数据和风化的未知类别玻璃文物数据,之后对表单2的数据规律按照风化和无风化进行总结,找到适合作为自变量的化学成分,确定自变量和因变量从而建立多元回归模型。
建立回归模型后再通过给予的未知类别玻璃文物数据计算出的预测结果并根据总结出来的数据规律判别是该化学成分属于高钾玻璃还是铅钡玻璃,最后根据哪一种类型可能性更大来决定该未知类别玻璃文物所属类型。
敏感性分析上更改各项系数中的一项,取附录2中数据代入计算,原计算结果与新数据的变化很明显,数据显著性很强。
2.4对问题四的分析
问题四属于相关性分析的问题类型,对于解决此类问题一般可以采用的分析方法包括多元线性回归模型,灰度分析等方法。
在问题一中,通过散点图和相关性分析可知,存在部分数据并不满足相关性,所以无法完全采用建立多元线性回归模型的方式完成分析,针对相关与不相关数据并存的情况,采用灰度关联分析的方式。求出相应的关联系数。
不同种类的玻璃其具有差异明显的化学成分关联关系,即具有对应关系系数,对关系系数进行排序,比较不同类别之间的化学成分关联关系的差异性。
三、模型假设
-
附件表2中缺失数据部分,视为含量极小可以忽略不计;
-
假设高钾玻璃和铅钡玻璃在分类之初不考虑风化对其的影响;
-
不同类型玻璃,自身突出特性对其他化学成分的掩盖影响在划分亚类时应当剔除;
-
假设实验数据允许存在一定的误差范围;
-
假设在做对比实验时遵循控制变量法,控制其他实验条件完全相同;
四、符号说明及名词定义
| 符号 | 定义 | 单位 |
|---|---|---|
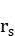 |
斯皮尔曼系数 | |
 |
等级差 | |
 |
多项式阶数 | 阶 |
 |
比例系数 | |
| ρ | 分辨系数 | |
| S | 总轮廓系数 | |
 |
关联度系数列表 |
五、模型的建立与求解
5.1问题一的求解与分析
5.1.1表面风化与玻璃类型、纹饰和颜色的关系
**Step1.**表单1数据可视化
为了对这些玻璃文物的表面风化与其玻璃类型、纹饰和颜色的关系进行分析,我们首先对表单里的数据进行可视化,使用Python的matplotlib分别展示表面风化与玻璃类型、纹饰和颜色的数量关系条形图。其中,表单1的58个数据中,有3个铅钡风化玻璃的数据它的颜色变量是没有数据的,由于风化后的化学成分变化是不确定的,并且使用完整的55个数据进行可视化分析对表面风化与颜色的关系猜测影响很小,故在该步骤下删去。

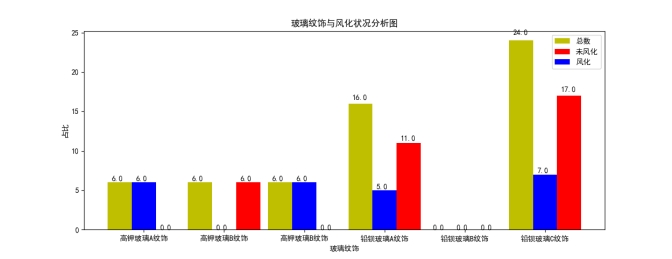
**Step2.**斯皮尔曼系数关联性分析
我们根据条形图的数量关系可以猜测表面风化与玻璃类型间的关系最大,与颜色和纹饰间的关系很小。皮尔逊系数进行关联性分析需要呈正态分布且是线性关系的连续变量,与表单1所给的定类变量而不是连续变量不符合。故我们选择利用斯皮尔曼系数,将定序数据划分等级0或1(风化或未风化,高钾或铅钡)、1~8(玻璃颜色)和1~3(玻璃纹饰)表示,运用公式(5-1)进行表面风化与玻璃类型、纹饰和颜色的关联性分析得出斯皮尔曼系数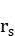 。设X,Y为两组数据,其中X为自变量X=(x1, x2, x3)=(类型,纹饰,颜色),Y为因变量是否表面风化,其斯皮尔曼(等级)相关系数:
。设X,Y为两组数据,其中X为自变量X=(x1, x2, x3)=(类型,纹饰,颜色),Y为因变量是否表面风化,其斯皮尔曼(等级)相关系数:
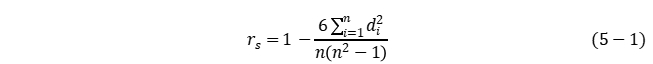
其中, 为
为 和之间的等级差。
和之间的等级差。
使用SPASS软件,计算斯皮尔曼相关系数,分析各变量与表面风化的关系。呈现结果如下表所示:
表5-1 斯皮尔曼系数
| 因变量 | 相关系数 | 表面风化 |
|---|---|---|
| 类型 | 相关系数 | 0.037 |
| Sig.(双尾) | 0.781 | |
| 纹饰 | 相关系数 | 0.344 |
| Sig.(双尾) | 0.008 | |
| 颜色 | 相关系数 | -0.107 |
| Sig.(双尾) | 0.442 |
通过表格可见,斯皮尔曼相关系数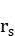
综上,表面风化和玻璃类型关系最大,和玻璃颜色与纹饰的关系不大。在接下来问题分析中,需要将玻璃类型考虑在内。
5.1.2文物样品表面有无风化化学成分含量的统计规律
**Step1.**表单2数据可视化
为了探究出文物样品表面有无风化化学成分含量的统计规律,我们统计出趋势、中位数、方差等。对数据进行均值比较和方差分析,根据结果使用Python进行数据可视化处理,画出无风化高钾玻璃和铅钡玻璃的化学成分比较折线图、高钾玻璃风化前后对比折线图和铅钡玻璃风化前后对比折线图进行观察。




综上,风化前和风化后的化学成分比例整体变化一致,我们可以针对变化明显的化学成分进行分析找到倍数关系。
**Step2.**表单2数据处理
根据题目内容可知表单2给出的相应的主要成分所占比例累加和介于 85%~105%之间的数据视为有效数据。通过Excel求和公式,计算出69个文物采样点的主要成分所占比例累加和。其中文物采样点15累加和为79.47%和文物采样点17累加和为71.89%,二者不在85%~105%之间,故剔除数据。
通过对表单2的数据分类整理可知,高钾玻璃都不含有氧化锡,可以在高钾玻璃中不考虑该化学成分。同时,风化后的高钾玻璃不含有氧化钠,氧化铅,氧化钡,氧化锶及二氧化硫这五种化学成分,无法寻找风化前和风化后的联系,化学成分预测上宜通过未风化中的化学成分规律。并且使用SPSS工具进行聚类分析,同样会优先将其中一种单独聚为一类,我们由此认定在该项聚类中,这部分数据没有意义,舍弃进行进一步聚类。
通过对风化前与风化后化学元素变化折线图5-5和5-6可知,铅钡玻璃中氧化钾、氧化铝、氧化铜、氧化锶风化前与风化后比例没有明显改变,可以认为风化前与风化后比例没有变化,在接下来分析中不做考虑。
对高钾玻璃和铅钡玻璃的剩余化学成分进行聚类分析,使用SPASS软件分析出化学成分集合分组,即由类似对象组成多个类的结果。处理结果如图5-4和图5-5所示。


5.1.3预测风化点在风化前的化学成分含量
**Step1.**高钾玻璃风化前的化学成分含量预测
根据相关性分析(分析结果见附录),二氧化硅和其他变量间都是强相关性,可以以二氧化硅为因变量,其他化学成分为自变量,对高钾玻璃的散点图进行曲线拟合。我们选择多项式曲线拟合进行少量数据的情况下拟合出比较好的曲线,原理如下:

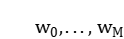 是多项式的系数,记作W。
是多项式的系数,记作W。
使用python软件的sklearn库和matplotlib库生成拟合图,如图5-4所示(文中仅展示部分代表,拟合发现同一类化学成分的曲线趋势基本相同)。



最后,对高钾玻璃中风化点在风化前的化学成分含量进行预测(W值在实际使用时小数点取前四位)。
对于前面分析中高钾玻璃采样点都不含有氧化锡所以该部分选择不填值。风化后的高钾玻璃不含有氧化钠,氧化铅,氧化钡,氧化锶及二氧化硫这五种化学成分,它们的化学含量占比小且最大差值小于2,我们可以用平均值表示这五个元素的化学含量。
对于二氧化硅的未风化预测,根据前面分析,我们可以用一个比例系数K 来通过风化值求出未风化的值,利用统计规律求解出比例系数K=0.7280。
对于剩下的七个化学成分我们通过拟合出来的函数进行求解。最终未风化前的化学成分含量预测结果如下表5-4所示。
**Step2.**铅钡玻璃风化前的化学成分含量预测
使用python软件的sklearn库和matplotlib库生成拟合曲线图,如图5-5所示:


根据上面聚类分析并结合表单2的统计学规律将铅钡玻璃所有变量划分为4个类,将其设为 。将铅钡玻璃中氧化钾、氧化铝、氧化铜、氧化锶风化前与风化后比例没有明显改变的4个变量的累加和设为定值
。将铅钡玻璃中氧化钾、氧化铝、氧化铜、氧化锶风化前与风化后比例没有明显改变的4个变量的累加和设为定值 。根据统计学规律计算出的系数设为
。根据统计学规律计算出的系数设为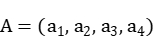
建立模型为:


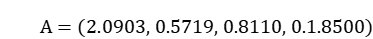 加入模型得:
加入模型得:

5.2问题二的求解与分析
5.2.1高钾玻璃、铅钡玻璃的分类规律

通过表单2中的数据分析风化前高钾玻璃和铅钡玻璃各化学成分含量并计算出均值。由上图均值比对可得出如下规律:高钾玻璃氧化钾的含量远高于铅钡玻璃,铅钡玻璃氧化铅和氧化钡的含量远高于高钾玻璃,以化学成分含量为依据而将其分为高钾玻璃和铅钡玻璃,分类标准合理。
5.2.2 数据预处理
在进行分类之前先进行数据的预处理。
玻璃的主要原料是石英砂,主要化学成分是二氧化硅(SiO2),所以二氧化硅这一化学成分的存在是古代玻璃所具有的共性,故将二氧化硅这一化学成分不作为分类依据。另外,针对不同类型的玻璃在分类时考虑自身突出特性对其他化学成分的掩盖影响应当剔除,由此铅钡玻璃在进行内部分类时,氧化铅和氧化钡不作为分类依据。同理,高钾玻璃在进行亚分类时氧化钾不作为分类依据。
数据来源上,将附件中表单2原始数据处理为高钾未风化、高钾风化、铅钡风化、铅钡无风化四种类型。根据假设条件,玻璃的分类是在完整未经风化状态下进行的,故而不考虑风化后的玻璃样本而将着眼点放在风化前的各样本数据上,这其中也包括了表面风化但局部未风化的样本即含有未风化点的样本,如23、25、28、29号文物等。经过数据剔除,最终考虑的样本数量状态为:无风化高钾玻璃12个样本,无风化铅钡玻璃23个样本。接下来对这些样本进行亚类划分。
5.2.3 亚类划分
本文通过SPSS软件,采用系统聚类模型分别针对高钾和铅钡玻璃进行亚分类。
系统聚类分析将各样品各看成一类,然后计算类与类之间的距离,选择距离最小的一对合并为新类,计算新类与其他各类的距离,再将距离最近的两类合并,这样依次迭代,直到所有样品合为一类为之,由此实现不同样本之间的聚类。



另外,在亚类划分时要考虑适合的化学成分,意即在划分完成后仍需进一步分析系统聚类结果中化学成分的内在联系,由此,在聚类完成后加入主观统计学分析,以系统聚类分析的结果为基础,与均值的比对为指引,寻找同一类样本之间化学成分上的联系,进而总结出规律,必要时可以重新组合类。
下面首先进行系统聚类分析:

注:03.1代表03部位1;03.2代表03部位2;30.1代表30部位1;30.2代表30部位2;
结合上图聚类结果将12个样本分为3类,分类结果如下:
之后进行统计学分析,观察各类之中有无化学成分含量突出或远高于均值的,抽象出分类标准。经过化学成分分析统计,比对得出高钾的三种分类标准:低铅钡、高磷、高铜。
同理,对于铅钡玻璃进行如下划分。

而后通过excel分析聚类中各化学成分含量,与均值进行比较得出5种分类标准:高磷、高钠、高铝、钙铁、高铜。
5.2.4合理性和敏感性检验
本文使用轮廓系数进行合理性检验,遍历簇数,计算对应轮廓系数,选择轮廓系数最大时对应的聚类模型。
单一轮廓系数:

聚类总体轮廓系数:

敏感性分析上,将具有典型化学成分含量特征的样本加入数据集,再次进行聚类分析,观测聚类结果是否与预料当中相同。本文中将问题一中预测的风化前的数据加入到高钾风化前、铅钡风化前的表单中进行聚类分析。分析是否与预期一致。
5.3问题三的求解与分析
5.3.1鉴别未知类别玻璃文物所属类型
观察表单3所给出的未知类别玻璃文物数据发现,每条数据分为文物编号、表面风化和化学成分3个变量,我们判别玻璃文物类型前可以先将数据划分为无风化的未知类别玻璃文物数据和风化的未知类别玻璃文物数据,然后再次对表单2的数据规律按照风化和无风化进行总结,找到合适作为自变量的化学成分,通过给予的未知类别玻璃文物数据和后期回归方程模型的建立计算出的预测结果,根据总结出来的数据规律判别是该化学成分属于高钾玻璃还是铅钡玻璃。最后根据哪一种类型可能性更大来决定该未知类别玻璃文物所属类型。
Step1 表单2数据规律分析
在建立多元回归方程模型的时候发现,14个化学成分的比例分布不平衡,如果按照将显著性最大的二氧化硅作为因变量之一,来建立多元回归模型的话会导致影响因变量的自变量只有二氧化硅甚至使用的自变量皆无意义,无法将其余13个化学成分的比例价值凸显出来,进而能准确利用结果进行未知类别玻璃文物所属类型的鉴别。所以我们转而对表单2的数据间统计规律进一步深究,使用能显著代表文物类型且非二氧化硅的化学成分。
首先对于表单2的数据我们先划分为风化和无风化两个大类,在其中又分四小类分别是无风化高钾玻璃、无风化铅钡玻璃、无风化铅钡玻璃和风化铅钡玻璃。通过Python软件的matplotlib库画出箱图展现每一个小类中一维变量的统计规律。如下图5-16所示。

之后根据箱图展现的统计规律和散点图展现的分布情况,进行以鉴别玻璃类型为目的数据整理,如下表5-12所示。
通过表5-12可知,高钾玻璃和铅钡玻璃的部分相同化学成分的变化范围是不相交的且存在明显的差异,我们可以在使用模型前直接判断出它的类型。同时可以将数据分类:第一类数据变化范围大,数值大可以考虑作为因变量,如未风化高钾的氧化铅和氧化钡;第二类数据整体波动适中,只出现几个较大值或较小值,可以考虑作为因变量或自变量,如氧化铜、氧化铁和氧化铝;第三类数据波动小且整体数值也小,还具有可以判别文物类型的特点,一般将其作为自变量,计算出的结果可以尽可能在表5-x的范围内,如未风化高钾的氧化锶。
Step1 2多元回归模型求取文物所属类别
多元回归模型基本形式为:

在无风化高钾玻璃类别中,我们使用SPASS软件进行多次计算,获得如下回归模型分析表5-13。
因变量:氧化钙
预测变量:(常量),氧化铝,氧化钡,氧化铅
| 预测变量 | B | t | 显著性 | VIF |
|---|---|---|---|---|
| (常数) | -2.103 | -3.145 | 0.006 | |
|  | 0.121 | 5.195 | 0.000 | 1.300 |
|  | -0.036 | -1.048 | 0.310 | 1.218 |
|  | 0.261 | 4.987 | 0.000 | 1.275 |


预测变量:(常量),氧化铝,氧化钡,氧化铅
| 预测变量 | B | t | 显著性 | VIF |
|---|---|---|---|---|
| (常数) | -1.782 | -1.613 | 0.125 | |
|  | 0.024 | 0.596 | 0.559 | 1.404 |
|  | 0.303 | 8.550 | 0.000 | 1.061 |
|  | 0.039 | 0.539 | 0.678 | 1.475 |


预测变量:(常量),氧化铝,氧化钡,氧化铅,氧化铜
表5-15 回归方程分析表
| R | R方 | 调整后R方 | 德宾-沃森 | 显著性 | |
|---|---|---|---|---|---|
|  | 0.904 | 0.818 | 0.785 | 1.260 | 0.000 |
| 预测变量 | B | t | 显著性 | VIF |
|---|---|---|---|---|
| 常数 | 1.504 | .241 | .891 | |
| 氧化铅 | -.047 | -.401 | .705 | 5.436 |
| 氧化钡 | .249 | .779 | .471 | 6.629 |
| 氧化铜 | 1.191 | 2.652 | .045 | 1.476 |
| 氧化铝 | -.059 | -.208 | .843 | 11.614 |

图5-20 氧化钠直方图 图5-21 氧化钠正态P-P图
因变量:氧化钡 预测变量:(常量),氧化铜
表5-16 回归方程分析表
| R | R方 | 调整后R方 | 德宾-沃森 | 显著性 | |
|---|---|---|---|---|---|
|  | 0.902 | 0.813 | 0.803 | 1.118 | 0.000 |
| 预测变量 | B | t | 显著性 | VIF |
|---|---|---|---|---|
| 常数 | 4.658 | 6.213 | 0.000 | |
| 氧化铜 | 2.718 | 9.091 | 0.000 | 1.000 |

图5-22 氧化钡直方图 图 5-23 氧化钡 P-P图
以上分析可知,所有的显著性都满足小于0.05的条件,故多元回归方程可行。在无风化条件下,如果以上化学成分不满足高钾玻璃的情况,那么将其归类为铅钡玻璃。在风化条件下,我们发现可以看高钾玻璃的成分情况与数据规律统计表对比,如果不符合高钾玻璃则为铅钡玻璃。
将表单3数据输入,首先将数据分类为风化和未风化。分析风化数据我们首先依据数据规律统计表,如果符合就符合个数加1,通过对符合高钾和铅钡玻璃的条件的个数进行判断该未知文物类型。最终判断结果如表5-17所示。
表5-17 玻璃文物分类表
| 高钾玻璃 | 铅钡玻璃 | |
|---|---|---|
| A2 | 6 | 2 |
| A5 | 1 | 6 |
| A6 | 8 | 0 |
| A7 | 7 | 0 |
但A2表数据缺失较多,但是含有类型特征较强的氧化铝,氧化铅,五氧化二磷3种化学成分,形成新的比例:高钾玻璃:铅钡玻璃=1:2,所以A2更可能是铅钡玻璃。
分析未风化数据,我们首先利用回归方程进行计算得:
| 氧化钠 | 氧化钙 | 氧化铜 | 氧化钡 | |
|---|---|---|---|---|
| A1 | 3.59044 | -0.21597 | -1.50003 | 10.39298 |
| A3 | -0.27902 | 3.28207 | 0.70326 | 5.22878 |
| A6 | 1.08907 | 2.38099 | 1.59438 | 7.26728 |
| A7 | 11.11155 | 0.61212 | 2.24646 | 29.14718 |
综上,高钾玻璃分别是A1,A4,A6,A7,铅钡玻璃分别是A2,A3,A5,A8
5.4问题四的求解与分析
我们可以使用灰色关联分析的方式对比较不同类别之间的化学成分关联关系的差异性
5.4.1 数据无量纲化处理
将题目给出表单2中,原始分类中的未经过风化的高钾玻璃与铅钡玻璃的数据分别导入SPSS,并通过Z-score标准化法对其中各项数据进行无量纲化。
Z-score标准化法公式如下:

Z-score标准化法,首先计算该指标的均值和标准差,然后用该变量的每一个观察值x减去均值x,再除以其标准差。
数据经过Z-score标准化后,将符合标准正态分布(0-1),即将有约一半观察值的数值小于0,另一半观察值的数值大于0,变量的均值为0,标准差为1,在本题的求解过程中,数据的标准化通过SPSS软件对数据分析获取[4]。
5.4.2 灰色关联分析不同类别之间的化学成分关联关系
将数据转置生成如下矩阵:

其中参数m是变量类型,结合表单2可知,在当前数据集下m=14
关联程度实质是参考数列与比较数列曲线形状的相似程度。凡比较数列与参考数列的曲线形状接近,则两者间的关联度较大;反之,如果曲线形状相差较大,则两者间的关联度较小。因此,可用曲线间的差值大小作为关联度的衡量标准。


其中ρ为分辨系数,用于降低Δ(max)过大而使关联系数出现较大误差,其取值范围(0,1)。当ρ越小,关联系数间差异越大,区分能力越强。在实现过程中ρ取值为0.5.
在本题的求解过程中,通过Matlab编程实现计算每个被评价对象指标序列,参考序列对应元素的绝对差值,并最终求出关联系数,并对其进行排序。(实现代码见附录)
5.4.3 差异性分析
最后对关联度进行排序,得到相应类型下的关联度顺序。
其中高钾玻璃的关联度系数列表为:
Gld = [23.0000 19.0240 18.1279 18.2748 19.2907 20.5374 19.9724 18.3470 18.1501 17.0090 16.9629 18.5236 20.0456 21.3854]对应的关联度顺序为:1,7,13,3,11,5,2,4,12,8,10,9,6,14
不同的是铅钡玻璃的关联度系数列表为:
Gld = [23.0000 21.3854 20.5374 20.0456 19.9724 19.2907 19.0240 18.5236 18.3470 18.2748 18.1501 18.1279 17.0090 16.9629]对应的关联度顺序为:1,14,6,13,7,5,2,12,8, 4,9 ,3,10,11
比较二者关联度顺序,即可证明不同类别之间的化学成分关联具有显著差异性
六、模型的评价与推广
6.1模型的优点
在分析文物样品表面有无风化化学成分含量的统计规律时,将整个决策过程分为两部分,分别基于多元回归和最小二乘法进行拟合,保证了数据分析结果的可靠。
在实现系统聚类后,对于一些规律不很明显的组合适当进行人工干预重新组合,提炼出分类特征从而形成类标签,实现基于化学成分的亚类划分。
使用灰色关联分析方式能够很好的处理部分信息未知、部分信息已知的数据。
6.2 模型的缺点
进行亚类划分时,系统聚类完成后又加以统计学分析,对于一些规律不很明显的组合进行人工干预重新组合,虽然有利于划分,但在客观上也导致了模型主观性成分的提高。
6.3 模型的优化
题目附件中数据量较少,随着建模过程的不断深入及划分亚类之后,每种亚类之间的数据量也过少,划分有较大误差。可以通过获取更大数据集对模型进行优化。
七、参考文献
[1] 李青会,干福熹 .关于中国古代玻璃研究的几个问题[J]. 自然科学史研究,2007年,26卷:234-247
[2] 段浩,干福熹,赵虹霞.实验室模拟过渡金属离子掺杂的中国古代玻璃的着色现象[J]. 硅酸盐学报 2009年12期
[3] 孙林,刘梦含,徐久成.基于优化初始聚类中心和轮廓系数的K-means聚类算法[J].模糊系统与数学,2022,36(01):47-65.
[4] 孙芳芳.浅议灰色关联度分析方法及其应用[J].科技信息, 2010
附录
附录说明:
-
各类玻璃元素对比组成可视化python实现
-
高钾玻璃各组成成分的拟合曲线python实现代码
-
对高钾玻璃、铅钡玻璃进行亚分类的划分结果
-
灰色关联分析Matlab代码实现
-
表单2数据规律统计表
附录1 各类玻璃元素对比组成可视化python实现
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
#字体设置为黑体
matplotlib.rcParams['font.family'] = 'SimHei'
matplotlib.rcParams['axes.unicode_minus'] = False
str1 = ("二氧化硅","氧化钠","氧化钾","氧化钙","氧化镁","氧化铝","氧化铁","氧化铜","氧化铅","氧化钡","五氧化二磷","氧化锶","氧化锡","二氧化硫")
y1=[68.71125,0,9.031428571,5.541428571,1.462857143,6.8525,2.768571429,2.895,0.642,1.795,1.75,0.0975,0,0.406666667]
y2=[94.286,0,0.84,0.712,0.54,1.616,0.248,1.764,0,0,0.3675,0,0,0]
y3=[62.095,2.48,13.525,8.485,0.52,6.17,1.65,2.9,0.11,0,1.27,0.04,0,0]
y4=[62.47,3.38,12.28,8.23,0.66,9.23,0.5,0.47,1.62,0,0.16,0,0,0]
x = [1,2,3,4,5,6,7,8,9,10,11,12,13,14]
plt.xticks(x, str1, rotation=45)
plt.plot(x,y1)
plt.plot(x,y2)
plt.plot(x,y3)
plt.plot(x,y4)
plt.show()附录2 高钾玻璃各组成成分的拟合曲线python实现代码
import numpy
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
#实例化线性模型****
lr = LinearRegression()
x=[69.33,87.05,61.71,65.88,61.58,67.65,59.81,92.63,95.02,96.77,94.29,92.35,92.72,59.01,65.18,62.47]
y=[9.99,5.19,12.37,9.67,10.95,7.37,7.68,0,0.59,0.92,1.01,0.74,0,12.53,14.52,12.28]
y2=[3.93,4.06,5.5,6.44,7.5,11.15,10.05,1.98,1.32,0.81,1.46,3.5,2.51,6.16,6.18,9.23]
y3=[3.87,0.78,5.09,2.18,3.27,2.51,2.18,1.56,1.55,0.84,1.65,0.55,1.54,4.73,1.07,0.47]
plt.xlabel('二氧化铜含量')
plt.ylabel('氧化铜含量')
plt.title('二氧化硅与氧化铜含量散点拟合曲线')
mymodel = numpy.poly1d(numpy.polyfit(x, y2, 4))
myline = numpy.linspace(60, 100, 100)
plt.scatter(x, y2) # 原始散点图
plt.plot(myline, mymodel(myline))
# 多项式回归
plt.show()
print(numpy.polyfit(x, y2, 4))附录3 对高钾玻璃、铅钡玻璃进行亚分类的划分结果
高钾玻璃

铅钡玻璃

附录4 灰色关联分析Matlab实现代码
x1 = [0.97731 1.29178 0.74085 0.1866 -0.60495 -0.45975 -0.96173 -0.19092 2.43346 0.39734 -0.49958 0.05052 -0.21996 0.14428 -0.1428 -0.57176 0.42721 0.11773 -1.71013;
-0.37264 3.74896 2.18943 -0.37264 -0.37264 -0.37264 -0.37264 -0.37264 1.11262 -0.37264 -0.37264 -0.37264 -0.37264 1.89238 -0.37264 -0.37264 -0.37264 -0.37264 -0.37264;
0.26337 -0.0789 -0.51452 -0.51452 -0.51452 0.85457 -0.51452 -0.51452 0.48118 -0.51452 -0.51452 -0.51452 -0.51452 -0.51452 0.48118 -0.51452 -0.51452 -0.51452 0.54342;
-1.01049 -1.2482 -1.06847 -0.81916 -0.37852 1.41303 1.57537 2.24792 0.17228 1.19271 0.3868 0.61292 1.51159 -0.1466 0.3868 -1.46272 -0.76118 -0.7032 0.56074;
-0.86124 -0.86124 -0.86124 -0.86124 -0.86124 3.03422 0.40871 0.49432 1.3362 1.23631 -0.19059 0.83678 1.20778 -0.07644 0.9652 0.72263 -0.86124 -0.86124 0.26602;
-0.53585 -0.54356 -0.16943 -0.96783 -0.98711 0.1237 -0.29286 0.15456 4.10411 0.91438 -0.43942 0.86424 -0.19257 -0.71327 0.43997 0.24712 -0.44714 -0.31985 0.19698;
-0.18267 -0.38351 -0.42368 -0.81198 -0.55758 1.58475 0.20563 1.04917 0.92866 2.85676 -0.37013 0.78138 -0.24962 -0.50402 -0.81198 -0.81198 -0.81198 -0.81198 0.33952;
-0.21803 -0.63577 -0.6106 -0.53511 -0.97801 -0.88238 1.71462 -0.21803 -0.97801 -0.6257 -0.40929 -0.2885 -0.60054 -0.6257 -0.56027 -0.30359 -0.58041 -0.39419 0.5973;
0.54957 0.22954 0.72837 1.50511 -1.99899 0.39214 1.41118 0.43296 -1.44834 -0.2518 0.38437 -2.19139 0.85988 0.60593 1.12678 1.32113 0.20622 0.45563 0.08313;
-1.00644 -0.92412 -0.13464 -0.38953 -0.4421 -0.13761 -0.38259 -0.78229 -0.38061 -0.50061 0.30275 -0.21894 -1.10562 -0.2487 -0.37168 -1.10562 0.42672 0.61021 -0.34589;
-1.16317 -1.07604 -1.12929 -0.96471 -0.81708 0.56002 -1.24546 1.85967 -0.97923 1.44097 0.28896 0.71491 0.87223 0.13648 -0.21929 2.1743 -0.63072 -1.24546 0.93031;
-0.70924 -0.70924 -0.03905 0.66641 0.91332 0.17259 0.77223 0.17259 -0.60342 0.13731 0.84278 -0.1096 -1.48525 0.06677 1.61879 2.46535 -1.48525 -1.48525 -0.6387;
-0.2446 -0.2446 -0.2446 -0.2446 -0.2446 -0.2446 -0.2446 -0.2446 4.79574 -0.2446 -0.2446 1.56377 -0.2446 -0.2446 -0.2446 -0.2446 -0.2446 -0.2446 -0.2446;
-0.31198 -0.31198 -0.31198 -0.31198 -0.31198 -0.31198 -0.31198 -0.31198 -0.31198 -0.31198 -0.31198 -0.31198 -0.31198 -0.31198 -0.31198 -0.31198 -0.31198 -0.31198 -0.31198;
]
%原始数据14行19列
x=x1;
for i=1:14
for j=1:19
x(i,j)=x(i,j)/x1(1,j)
end
end
x1=x
for i=1:14
for j=1:19
x(i,j)=abs(x(i,j)-x1(i,1))
end
end
max=x(1,1)
min=x(1,1)
for i=1:14
for j=1:19
if x(i,j)>=max
max=x(i,j)
end
end
end
for i=1:14
for j=1:19
if x(i,j)<=min
min=x(i,j)
end
end
end
k=0.5 %分辨系数取值
l=(min+k*max)./(x+k*max)%求关联系数矩阵
guanlianxing=sum(l')/1
[rs,rind]=sort(guanlianxing,'descend') %对关联度进行排序
