Matlab相关知识 | 十二惊惶

学习笔记

发布日期: 2022-01-10

更新日期: 2025-04-26

文章字数: 12.1k

阅读时长: 45 分

阅读次数:

Matlab入门

[TOC]

1.Matlab系统环境

Matlab主窗口：

**功能区：**提供三个选项卡（主页，绘图，应用程序），各自有不同的工具可供使用；快速访问工具栏：包含一些常用按钮；当前文件夹工具栏：用于实现当前文件夹的操作。一定要先建立文件再将其设为工作文件夹。

命令行窗口

命令行窗口用于输入命令并显12示命令的执行结果。在命令提示符 $>>$ 后输入命令并按下回车键，Matlab就会解释执行输入的命令并显示结果。如果命令行很长可以在第一个命令行后面加三个小数点…在下一行继续输入命令的其他部分，这三个…称为续行符，用于将下一行的命令视为这一行命令的逻辑相连

工作区窗口： 是Matlab用于存储各种变量和结果的空间，可用于变量的显示和操作。在工作区以表格形式显示变量a与x的名称，取值等信息。在工作区还可以对变量进行保存、编辑、删除等操作

设置文件搜索路径

MATLAB是在当前文件夹与搜索路径文件夹中寻找这个文件并执行文件内容的，所以要执行的文件必须放在这两类文件夹中。

使用path命令设置文件搜索路径
用对话框设置文件搜索路径
- 当前文件夹与搜索路径文件夹下均有同名m文件，会执行当前文件夹下的m文件

2.Matlab的数值数据

**整型 : **

无符号整数:无符号8位整数、无符号16位整数、无符号32位整数、无符号64位整数.带符号整数:带符号8位整数、带符号16位整数、带符号32位整数、带符号64位整数。

浮点型：

浮点型数据分为单精度型和双精度类型，单精度型实数在内存中占用4个字节，而双精度型实数在内存中占用8个字节，所以双精度型的数据精度更高

single函数：将其他类型的数据转换为单精度型

double函数：将其他类型的数据转换为双精度型

class函数：可以得到参数的数据类型

复型数据包括实部和虚部两个部分，实部和虚部默认为双精度型，虚数单位用i或|来表示

real() %求复数的实部
imag() %求复数的虚部

数值数据的输出格式

Matlab可以用format函数设置数值数据的输出格式，

format 格式符  % 设置数据的输出格式

不同的格式符输出不同的数据格式，同时format命令只是影响数据输出的格式，而不影响数据的计算和存储。

常用数学函数

函数的调用格式为：

函数名（函数自变量的值）

函数的自变量规定为矩阵变量（标量本身是矩阵的一种特例）

函数在运算时是将函数逐项作用于矩阵的每个元素上，所以最后运算的结果就是一个与自变量同型的矩阵。

常用函数

三角函数有以弧度为单位的函数和以角度为单位的函数,如果是以角度为单位的函数就在函数名后面加d，以示区别

abs函数可以求实数的绝对值、复数的模、字符串的ASClI码值

用于取整的函数有fix、floor、ceil、round

round函数按照四舍五入的规则取整
ceil函数是向上取整，取大于等于这个数的第一个整数
floor函数是向下取整，取小于等于这个数的第一个整数
fix函数是固定取靠近0的那个整数,即舍去小数取整

isprime(n) # 判断n是否是素数，是返回1，否返回0.

3.变量及其操作

计算机处理的数据都是存放在内存单元中的，而每一个内存单元都有一个唯一的地址，程序就是通过这个地址来访问对应内存单元的
在如Matlab这种高级语言中，只需要给每个内存单元取一个名字，然后通过这个名字就能访问每个内存单元了

变量与赋值语句

变量本质上讲是内存单元的一个抽象
在Matlab中，变量名是以字母开头，后接字母、数字或下划线的字母序列，最多63个字符。

赋值语句两种格式

变量=表达式        % 变量结果会在命令行中显示出来
变量=表达式；	  % 变量结果不会在命令行中显示出来

Matlab语言还有一些预定义的变量，预定义变量是由系统本身定义的变量。如ans是默认赋值变量，i和j代表虚数单位，pi代表圆周率，NaN代表非数

变量的删除和修改（who,whos）

在工作区选择变量右击即可进行删除和修改

who命令和whos命令：who命令只显示已存在变量的名称。而whos显示包括变量类型，长度等信息

内存变量文件(save,load)

用于保存Matlab工作区变量的文件叫做内存变量文件，其扩展名为.mat，也叫MAT文件，是一种标准的二进制格式文件
save命令：创建内存变量文件 load命令：载入内存变量文件

save mydata a x   % 将a x保存在mydata.mat文件中
load mydata       % 载入mydata.mat中的变量

4.MATLAB矩阵表示

矩阵的建立

冒号表达式：

1 用冒号产生行向量t：

t=0:1:5 %格式为： 初始值：步长：终止值

2 用linspace函数产生行向量x:

x=linspace(a:b:n)%(第一个元素：第二个元素：总数)

如果n忽略不写则自动生成100个数据。

结构矩阵和单元矩阵

结构矩阵：

在实际应用中，经常会遇到不同类型的数据项组成的实体，例如一个学生的数据实体就包括了年龄，姓名，学号，这些数据是相互联系的。结构数据类型就可以把这些数据类型不同但逻辑上相关的数据组成一个有机的整体。

结构矩阵元素.成员名=表达式

单元矩阵：

单元数据类型，也是把不同的数据放在一个变量中，但与结构矩阵所不同的是，结构矩阵的各个元素下还有成员，每个成员都有自己的名字，而单元矩阵的各个元素就是不同类型的数据，每个元素直接由不同类型的数据组成。

5.矩阵元素的引用

5.1 常规矩阵

1 通过下标来引用矩阵的元素

**2 通过序号来引用：**在MATLAB中，矩阵元素按列存储，即首先存储矩阵的第一列元素，然后存储第二列元素，一直到矩阵的最后一列元素。矩阵元素的序号就是矩阵元素在内存中的排列顺序。

序号与下标是一—对应的，以m×n矩阵A为例，矩阵元素A(i.j)的序号为(j-1)×m+i。矩阵元素的序号与下标可以利用sub2ind和ind2sub函数实现相互转换。

sub2ind函数:将矩阵中指定元素的行、列下标转换成存储的序号。调用格式为:

D=sub2ind(S,I,J)%  S行数和列数组成的向量  I转换矩阵元素的行下标  J转换矩阵元素的列下标

ind2ind函数:将矩阵元素的序号转换成对应的下标，调用格式为:

[I,J]=ind2sub(S,D)% I行下标 J列下标 S行数和列数组成的向量 D序号

3 利用冒号表达式获得子矩阵(end)

子矩阵是指由矩阵中一部分元素构成的矩阵。

end运算符：表示某一维的末尾元素下标

可以利用空矩阵删除矩阵的元素，

4.改变矩阵的形状(reshape)

在矩阵总元素保持不变的前提下，将矩阵A重新排成 $m*n$ 的二维矩阵。

reshape (A,m,n)

注意：reshape函数只是改变原矩阵的行数和列数，但并不改变原矩阵元素个数及其存储顺序。

A(:)将矩阵A的每一列元素堆叠起来成为一个列向量。

A(:)等价于 reshape(A,6,1)

5.2 特殊矩阵：

5.2.1 通用性矩阵：

以上函数调用格式相同，以zeros为例：

5.2.2 对角阵：

**对角矩阵：**只有对角线上有非零元素的矩阵
**数量矩阵：**角线上元素相等的对角矩阵
**单位矩阵：**对角线上元素都为1的对角矩阵

diag(a)  %提取矩阵A主对角线元素，产生一个列向量
diag(a,k) %提取矩阵A第k条对角线的元素，产生一个列向量。

diag函数也可以构造对角矩阵：

diag(V) %一向量V为主对角线元素，产生对角矩阵。
diag(V,k) %以向量V为第k条对角线元素，产生对角矩阵。

5.2.3 三角阵：

上三角矩阵:

triu(A)  %提取矩阵A的主对角线及以上的元素。
triu(A,k)%提取矩阵A的第k条对角线及以上的元素。

下三角矩阵：在MATLAB中，提取矩阵A的下三角矩阵的函数是tril，其用法与triu函数完全相同。

5.2.4 用于专门学科的特殊矩阵

魔方矩阵Magic Square

n阶魔方阵由1,2,3,…,n2共n2个整数组成，且每行,每列以及主副对角线上各n个元素之和都相等。n阶魔方阵每行每列元素的和为**(1+2+3+…+ n^2)/n=(n+n^3)/2**。MATLAB函数magic(n)产生一个特定的魔方阵

在MATLAB中，函数vander(V)生成以向量V为基础的范得蒙 Vandermonde矩阵。

范德蒙矩阵常用于各种通信系统的纠错编码中

在MATLAB中，生成n阶希尔伯特矩阵的函数是hilb（n）

希尔伯特矩阵正定，且高度病态（即，任何一个元素发生一点变动，整个矩阵的行列式的值和逆矩阵都会发生巨大变化），病态程度和阶数相关。

MATLAB生成伴随矩阵的函数是compan§，其中p是一个多项式的系数向量，高次幂系数排在前，低次幂系数排在后。

帕斯卡矩阵的第一行元素和第一列元素都为1，其余位置的元素是该元素的左边元素与上面元素相加，即P(i,j)=P(i,j- 1)+P(i-1,j)，且P(i,1)=1,P(1,j)=1。函数pascal(n)生成一个n阶帕斯卡矩阵。

5.3 矩阵变换

矩阵的转置：

转置运算符是小数点后面接单引号 .'
共扼转置E，其运算符是单引号 ’ 它在转置的基础上还要取每个数的复共轲。

矩阵的翻转：

rot90(A,k) :将矩阵A逆时针方向旋转90°的k倍，当k为1时可省略

fliplr(A) :对矩阵A实施左右翻转。flipud(A) :对矩阵A实施上下翻转

矩阵的求逆：

对于一个方阵A，如果存在一个与其同阶的方阵B，使得AB=BA=l(I为单位矩阵)，则称B为A的逆矩阵，A也是B的逆矩阵

**inv(A) ** : 求方阵A的逆矩阵

6.Matlab基本运算

6.1算数运算

基本算数运算

基本算术运算符:＋（加）、—（减）、*（乘） /（左除） \（右除）^乘方

MATLAB的算术运算是在矩阵意义下进行的。单个数据的算术运算只是矩阵运算的一种特例。

**加减运算:**若两矩阵同型，则运算时两矩阵的相应元素相加减。若两矩阵不同型，则MATLAB将给出错误信息,一个标量也可以和矩阵进行加减运算，这时把标量和矩阵的每一个元素进行加减运算.

**乘法运算：**矩阵A和B进行乘法运算，要求A的列数与B的行数相等，此时则称A、B矩阵是可乘的，或称A和B两矩阵维数和大小相容。如果两者的维数或大小不相容，则将给出错误信息，提示用户两个矩阵是不可乘的。

除法运算：在MATLAB中，有两种矩阵除法运算:右除/和左除\。如果A矩阵是非奇异方阵，则B/A等效于B * inv(A)，A\B等效于inv(A) * B。对于矩阵来说，右除和左除表示两种不同的除数矩阵和被除数矩阵关系。

左除： A / B = A * B ^ -1
右除： A \ B = A ^ -1 * B

**乘方运算：**一个矩阵的乘方运算可以表示成A^x，要求A为方阵，x为标量。

点运算

**点运算:**两矩阵进行点运算是指它们的对应元素进行相关运算，要求两矩阵同型。Matlab中的点运算，就是对矩阵中的元素一一运算，基本的点运算有点乘、点除、点幂。

点运算与算数运算的区别 .* 点乘：将每个元素乘以一个数

./ (左点除) ：将每个元素除以一个数或者矩阵。如A ./ B A,B对应元素相除。(在点除的时候需要保证矩阵形式相同)

.\ (右点除) :

A.\3 %3除以A中对应元素
A.\ B%用每一个元素分别对应除以矩阵中的元素。

.^(点幂) ：

A.^1.2 %A中每个元素的1.2次方
A.^B   %A中每个元素作为底数，B中对应元素作为次数，进行幂运算
3.^B   %以3为底、B中元素为次数

Matlab用%表示注释。

6.2 关系运算:

<(小于)、<=(小于或等于)、>(大于)、>=(大于或等于)、==(等于)、~=(不等于)

当两个比较量是标量时，直接比较两数的大小。若关系成立，关系表达式结果为1，否则为0

当参与比较的量是两个同型的矩阵时，比较是对两矩阵相同位置的元素按标量关系运算规则逐个进行，最终的关系运算的结果是一个与原矩阵同型的矩阵，它的元素由0或1组成。当参与比较的一个是标量，而另一个是矩阵时则把标量与矩阵的每一个元素按标量关系运算规则逐个比较，最终的关系运算的结果是一个与原矩阵同型的矩阵，它的元素由0或1组成

6.3 逻辑运算

:&(与)、I(或)和～(非)

设参与逻辑运算的是两个标量a和b，那么运算规则为:a&b a、b全为非零时，运算结果为1，否则为0。alb a、b中只要有一个为非零时，运算结果为1。~a当a为零时，运算结果为1;当a为非零时，运算结果为0。

在算术运算、关系运算和逻辑运算中，算术运算的优先级最高，逻辑运算优先级最低，但逻辑非运算是单目运算，它的优先级比双目运算要高。单目是涉及一个元素的运算，双目是涉及两个的运算。

若参与逻辑运算的是两个同型矩阵，那么将对矩阵相同位置上的元素按标量规则逐个进行运算，最终运算结果是一个与原矩阵同型的矩阵，其元素由1或0组成。若参与逻辑运算的一个是标量，一个是矩阵，那么将在标量与矩阵中的每个元素之间按标量规则逐个进行运算，最终运算结果是一个与原矩阵同型的矩阵,其元素由1或0组成。

6.4 矩阵求值

矩阵的行列式

把一个方阵看作一个行列式，并对其按行列式的规则求值，这个值就称为方阵所对应的行列式的值。

det(A):求方阵A所对应的行列式的值

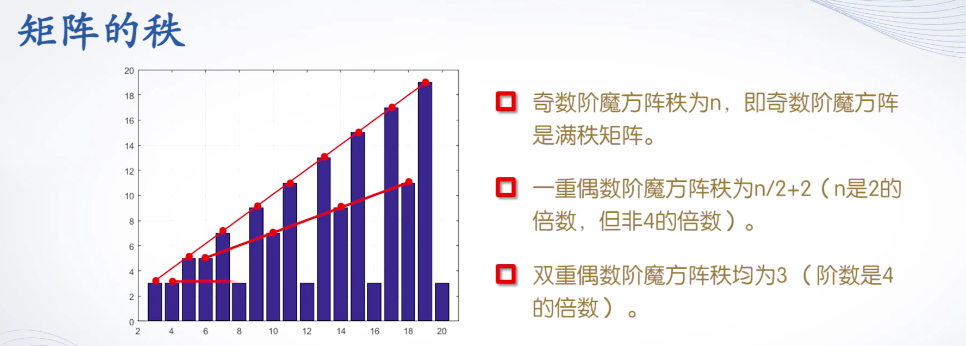
矩阵的秩

矩阵线性无关的行数或列数称为矩阵的秩。rank(A):求矩阵A的秩。

矩阵的迹

矩阵的迹等于矩阵的对角线元素之和，也等于矩阵的特征值之和。

trace(A)     %求矩阵A的迹。

**向量和矩阵的范数：**矩阵或向量的范数用来度量矩阵或向量在某种意义下的长度。

MATLAB提供了求3种矩阵范数的函数,其函数调用格式与求向量的范数的函数完全相同。

矩阵的条件数

矩阵A的条件数等于A的范数与A的逆矩阵的范数的乘积。条件数越接近于1，矩阵的性能越好，反之，矩阵的性能越差。

在MATLAB中，计算矩阵A的3种条件数的函数是:

cond(A,1)          %计算A的1一范数下的条件数。
cond(A)或cond(A,2) %计算A的2—范数下的条件数。
cond(A, inf)       %计算A的○o—范数下的条件数。

矩阵的特征值与特征向量

矩阵特征值的数学定义

求矩阵的特征值和特征向量

函数调用格式有两种：

E=eig(A) %求矩阵A的全部特征值，构成向量E
[X,D]=eig(A) %求矩阵A的全部特征值，构成对角阵D，并产生矩阵X，X各列是相应的特征向量。

稀疏矩阵

稀疏矩阵指的是零元素个数远远多于非零元素个数的矩阵，如果将大量的零元素也存储起来，必将导致存储空间的浪费。为此，MATLAB为稀疏矩阵提供特殊的存储方式。

矩阵的存储方式

1,完全存储方式

2,稀疏存储方式稀疏存储方式只存储矩阵的非零元素的值及其位置，即行号和列号。注意,采用稀疏存储方式时，矩阵元素的存储顺序并没有改变，也是按列的顺序进行存储。

稀疏存储方式的产生

(1)完全存储方式与稀疏存储方式之间的转化

A=sparselS)  %将矩阵S转化为稀疏存储方式的矩阵A。
S=full(A)    %将矩阵A转化为完全存储方式的矩阵S。

用A的一行元素表示一个稀疏矩阵的元素，相当于A每一行的每个元素是相应的稀疏矩阵元素的一个信息。这些信息组合经过spconvert就可以得到相应的稀疏矩阵元素。

(3)带状稀疏矩阵的稀疏存储
稀疏矩阵有两种基本类型:无规则结构的稀疏矩阵与有规则结构的稀疏矩阵。带状稀疏矩阵是指所有非零元素集中在对角线上的矩阵。
[B,d]=spdiags(A):从带状稀疏矩阵A中提取全部非零对角线元素赋给矩阵B及其这些非零对角线的位置向量d。
A=spdiags(B,d,m,n):产生带状稀疏矩阵的稀疏存储矩阵A，其中m、n为原带状稀疏矩阵的行数与列数，矩阵B的第i列即为原带状稀疏矩阵的第i条非零对角线，向量d为原带状稀疏矩阵所有非零对角线的位置。

(4)单位矩阵的稀疏矩阵

speye(m,n)   %返回一个m*n的稀疏存储单位矩阵。

稀疏矩阵应用举例

clc;clear
kf1= [1;1;2;1;0];     % 主对角线以下第一条元素
k0 = [2;4;6;6;1];     % 主对角线元素
k1 = [0;3;1;4;2];     % 主对角线以上第一条元素
B = [kf1,k0,k1];
d = [-1;0;1];
A = spdiags(B,d,5,5); % 产生稀疏存储的稀疏矩阵
f = [0;3;2;1;5];
x = A\f               %求出解

当参与运算的数据对象不全是稀疏储存矩阵时，所以结果是完全存储形式。

7.Matlab中的.m文件

.m文件分为两类

脚本文件，不传参数只执行计算等功能。

脚本文件只是一个计算模块，保存文件名时可以在满足命名规则的基础上任意命名。
函数文件，需要传参数，返回计算结果。

函数文件必须以关键字function开头，一般需要传参数和返回值，在保存是必须以函数名作为文件名保存。

注意在调用自己编写的函数时，调用的函数与被调用的函数必须放在同一文件夹下
脚本文件和函数文件可以相互转换

8.Matlab中的基本语句

条件语句

格式1 if end条件语句
格式2 if else end 条件语句
格式3 if else elseif end 条件语句
switch语句，适用于有更多选项的程序。
try语句try语句尝试执行语句1，如果在执行过程中出现错误，则转去执行语句组2.

循环语句

for-end循环，for循环变量由初值，步长和终值决定，内部为循环体语句。for语句更一般的格式为 for 循环变量=矩阵表达式，然后执行循环体语句直到各列元素处理完毕。

蒙特卡罗方法求概率，用随机数模拟实际过程的方法。

二分法求根的编程思路1,定义求根的函数2,主函数使用while循环比较合适。

Matlab中的数组下标是从1开始的。

Matlab以矩阵或向量为元素进行运算，可以减少循环，从而减少运行时间,点运算是Matlab的特点

符号对象

符号对象的建立

sym函数
syms命令

1 sym函数

sym函数用于建立单个符号对象，其常用调用格式为：符号对象名=sym(A)
将由A来建立符号对象。其中，A可以是一个数值常量、数值矩阵或数值表达式（不加单引号），此时符号对象为一个符号常量；A也可以是一个变量名（加单引号），这是符号对象为一个符号常量。

%例1 符号常量
>> t=sym(2);
>> t+1/2
>> sin(sym(pi/3))   %sin(sym(pi/3))得到的是一个表达式
>> sin(pi/3)   %sin(pi/3)得到的是一个数值

%例2 符号变量
>> a=5;
>> b=-8;
>> x=sym('a');
>> y=sym('b');
>> w=(a+b) * (a-b)
>> s=(x+y) * (x-y)

**结论：符号计算的结果是一个精确的数学表达式。数值计算的结果是一个数值。**将符号表达式转化为数值结果，使用eval()sym一次只能定义单个符号对象，如果符号对象很多，就不方便。

2 syms命令

syms命令可以一次定义多个符号变量，其一般调用格式如下：syms 符号变量1 符号变量2 ... 符号变量n

其中，变量名不能加单引号，相互之间用空格隔开。建立完符号对象，再用符号运算符连接起来，就组成了符号表达式。

符号对象的运算

<1>四则运算
符号表达式的四则运算与数值运算一样，用+、-、*、/运算符实现，其运算结果依然是一个符号表达式。

<2>关系运算

6种关系运算符：<、<=、>、>=、==、~=。
对应的6个函数：lt()、le()、gt()、ge()、ge()、eq()、ne()。

若参与运算的是符号表达式，其结果是一个符号关系表达式；若参与运算的是符号矩阵，其结果是由符号关系表达式组成的矩阵。

在进行符号对象的运算前，可用assume函数对符号对象设置域，函数调用格式为：
assume(condition)
assume(expr, set)

第一种格式指定变量满足条件condition，第二种格式指定表达式expr属于set

3 逻辑运算

3种逻辑运算符：&(与)、|(或)和~(非)
4个逻辑运算函数：and()、or()、not()和xor()

<4>因式分解与展开运算
MATLAB提供了对符号表达式进行因式分解、展开、合并的函数，函数的调用格式为：
fator(s)：对符号表达式s分解因式。

expand(s)：对符号表达式s进行展开。
collect(s)：对符号表达式s合并同类项。
collect(s, v)：对符号表达式s按变量v合并同类项。

5 其他计算

1 提取有理分式的分子分母：[n, d]=numden(s)
2 提取符号表达式的系数(低位到高位)：c=coeffs(s, x)
3 符号表达式化简：simplify(s)
4符号多项式与多项式系数向量之间的转换：
符号多项式转换为多项式系数向量：p=sym2poly(s)
多项式系数向量转换为符号多项式：s=ploy2sum()

f只能有一种符号变量

6 符号运算中变量的确定

如果没有明确指定自变量，MATLAB将按以下原则确定主变量并对其进行相应运算：
寻找除了i、j之外，在字母顺序上最接近x的小写字母。
若表达式中有两个符号变量与x的距离相等，则ASCII码大者优先。
symvar()函数可以用于查找一个符号表达式中的符号变量，函数的调用格式为：symvar(s,n)。函数返回符号符号表达式s中的n个符号变量。因此，可以用symvar(s, 1)查找表达式s的主变量。

符号矩阵

符号矩阵也是一种符号表达式，所以符号表达式运算都可以在矩阵意义下进行。
注意：这些函数作用于符号矩阵时，是分别作用于矩阵的每一个元素。

由于符号矩阵也是矩阵，所以有关矩阵的函数也可以使用。

符号微积分

符号函数的极限

1 符号函数的极限

求符号函数极限的命令limit，其调用格式为：limit(f, X, a)即求函数f关于变量x在a点的极限。若x省略，则采用系统默认的自变量。a的默认值为0。
limit函数的另一种功能是求单边极限，其调用格式为：
limit(f, x, a, 'right')
limit(f,x,a,'left')

符号函数的导数

MATLAB中的求导函数为：diff(f, x, n)
即求函数f关于变量x的n阶导数。参数x的用法同求极限函数limit，可以缺省，默认值与limit相同，n的默认值是1。

极限、导数、微分的概念是紧密关联的。有极限是可导的前提，而导数是微分之商，因此导数也称为微商。

符号函数的积分

1 不定积分

在MATLAB中，求不定积分的函数是int，其常用调用格式为：int(f, x)求函数f对变量x的不定积分。

2 定积分
在MATLAB中，定积分的计算也使用int命令，但调用格式有区别：int(f, a, b)
其中，a、b分别表示定积分的下限和上限。

当函数关于变量x在闭区间[a, b]可积时，函数返回一个定积分的结果。
当a、b中有一个是inf时，函数返回一个广义积分。
当a、b中有一个是符号表达式时，函数返回一个符号函数。

级数

级数求和

泰勒级数

MATLAB提供了taylor( )函数将函数展开为幂级数。其调用格式为:

taylor(f,v,a,Name,Value)

该函数将函数f按变量v在a点展开为泰勒级数,v省略时按默认规则确定变量,a的默认值是0。Name和Value为选项设置，经常成对使用，前者为选项名，后者为该选项的值。

符号方程求解

代数方程

在MATLAB中，求解用符号表达式表示的代数方程可由函数solve( )实现，其调用格式为:

solve(s):求解符号表达式s的代数方程，求解变量为默认变量。
solve(s,v):求解符号表达式s的代数方程，求解变量为v。
solvel(s1,s2… ,sn,vl,v2,…,vn):求解符号表达式s1，s2，… , sn组成的代数方程组，求解变量分别为v1，v2，…， vn。

常微分方程

数据统计分析

求最大值与最小元素

max(): 求向量或矩阵的最大元素
min():求向量或矩阵的最小元素

当参数为向量时函数有两种调用格式：

(1) y=max(X):返回向量X的最大值存入y，如果X中包含复数元素，则按模取最大值。

(2)[y,k]=max(X): 返回向量X的最大值存入y，最大值元素的序号存入k，如果X中包含复数元素，则按模取最大值。

%例1:
x=[-43,72,9,16,23,47];
y=max(x)
[y,k]=max(x)

当参数为矩阵时，函数有三种调用格式：

(1)max(A):返回一个行向量，向量的第i个元素是矩阵A的第i列上的最大值。
(2)[Y,U]=max(A):返回行向量Y和U，Y向量记录A的每列的最大值，U向量记录每列最大值元素的行号。
( 3 ) max(A,0,dim): dim取1或2。dim取1时，该函数的功能和max(A)完全相同;dim取2时，该函数返回一个列向量，其第i个元素是A矩阵的第i行上的最大值。其中的[]不可省略

%例二 求矩阵A的每行及每列的最大元素，并求整个矩阵的最大元素
max(A) %求每列的最大值
max(A,[],2) %将矩阵转置求每行的最大值
max(max(A)) %两次调用max函数，求整个矩阵的最大值
%在实际上，可以通过max(A(:))的调用方式，只用一次max函数就得到最大值。

求平均值和中值

平均值: 指算术平均值，即每项数据之和除以项数。
中值: 指在数据序列中其值的大小恰好处在中间的元素。如果数据个数为奇数，则取值为大小位于中间的元素;如果数据个数为偶数，则取中间两个元素的平均值。

mean()      % 求算术平均值
median（）  % 求中值

求和与求积

sum()    % 求和
prod（） % 求积

累加和与累乘积

cumsum(): 累加和函数，cumprod():累乘积函数。

求标准差与相关系数

std( ):计算标准差函数。

调用格式:

std(X):计算向量X的标准差。
std(A):计算矩阵A的各列的标准差。
std(A,flag,dim): flag取0或1，当flag=0时，按S所列公式计算样本标准差;当flag=1时，按Sz所列公式计算总体标准差。默认情况下，flag=0，dim=l。

corrcoef( ):相关系数函数。

调用格式:

corrcoef(A):返回由矩阵A所形成的一个相关系数矩阵，其中,第i行第j列的元素表示原矩阵A中第i列和第j列的相关系数。
corrcoef(X,Y):在这里，X、Y是向量，它们与corrcoef([X,Y)的作用一样,用于求X、Y向量之间的相关系数。

排序

sort( ):排序函数 调用格式:

sort(X):对向量X按升序排列。
[Y,I]=sort(A,dim,mode)

其中，dim指明对A的列还是行进行排序。mode指明按升序还是降序排序，若取“ascend”，则按升序;若取“descend”，则按降序，默认为升序。输出参数中，Y是排序后的矩阵，而l记录Y中的元素在A中位置。

多项式计算

多项式的表示

在MATLAB中创建多项式向量时，注意三点：

多项式系数向量的顺序是从高到低。
多项式系数向量包含0次项系数，所以其长度为多项式最高次数加1。
如果有的项没有，系数向量相应位置应用0补足。

多项式的四则运算

多项式的加减运算

多项式的加减运算非常简单，即相应向量相加减。

多项式乘法

conv (P1,P2):多项式相乘函数，在这里，P1、P2是两个多项式系数向量。

多项式除法

[Q,r]=deconv(P1,P2):多项式相除i函数。其中，Q返回多项式Pl除以P2的商式，r返回Pl除以P2的余式。这里，Q和r仍是多项式系数向量。deconv是conv的逆函数，因此有Pl=conv(Q,P2)+r

多项式的求导(polyder)

polyder( ): 多项式求导函数。

调用格式:

p=polyder§ : 求多项式P的导函数。
p=polyder(P,Q) : 求P · Q的导函数。
[p , q]=polyder(P,Q) : 求P/Q的导函数，导函数的分子存入p，分母存入q。

多项式积分(polyder)

q = polyint(p,k) 使用积分常量 k 返回 p 中系数所表示的多项式积分。

多项式的求值(polyval;polyvalm)

polyval(p,x)

其中，p为多项式系数向量;x可以是标量、向量或矩阵。若x为标量，则求多项式在该点的值;若x为向量或矩阵，则对向量或矩阵中的每个元素求多项式的值。
polyvalm(p,x)
其调用格式与polyval相同，但含义不同。polyvalm函数要求x为方阵，以方阵为自变量求多项式的值。

多项式的求根(roots;poly)

一元二次多项式求根: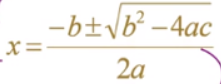

一元高次多项式求根： roots§: 多项式求根函数，其中，p为多项式的系数向量。

若已知多项式的全部根，则可以用poly函数建立起该多项式，其调用格式为： p=poly(x)

数据插值(interp)

数据插值可以根据有限个点的取值状况，合理估算出附近其他点的取值，从而节约大量的实验和测试资源，节省大量的人力、物力和财力。

数据插值的计算机制

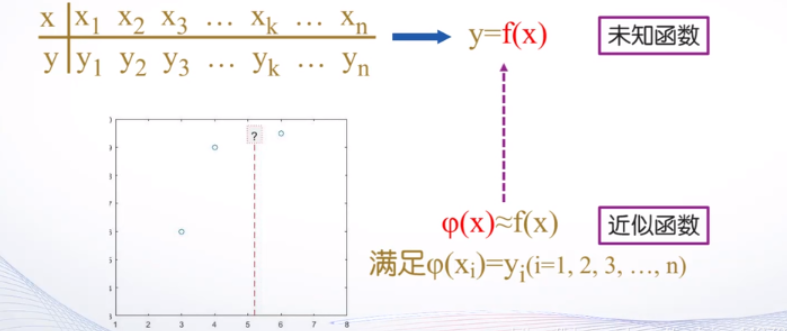
interp1( ):一维插值函数。

调用格式: Y=interp1(X,Y,X1,method)

根据X、Y的值，计算函数在×1处的值。其中，X、Y是两个等长的已知向量，分别表示采样点和采样值。Xl是一个向量或标量，表示要插值的点。

数据插值的实现方法

method用于指定插值方法，常用的取值有以下四种:

linear: 线性插值，默认方法。将与插值点靠近的两个数据点用直线连接，然后在直线上选取对应插值点的数据。
nearest: 最近点插值。选择最近样本点的值作为插值数据。
pchip: 分段3次埃尔米特抽值。米用分段三次多项式，乐满疋插值条件，还需满足在若干节点处相邻段插值函数的一阶导数相等，使得曲线光滑的同时，还具有保形性。
spline: 3次样条插值。每个分段内构造一个三次多项式，使其插值函数除满足插值条件外，还要求在各节点处具有连续的一阶和二阶导数。

多项式次数并非越高越好。次数越高，越容易产生震荡而偏离原函数，这种现象称为龙格(Runge）现象。

四种方法的比较：

线性插值和最近点插值方法比较简单。其中线性插值方法的计算量与样本点n无关。n越大，误差越小。
3次埃尔米特插值和3次样条插值都能保证曲线的光滑性。相比较而言,3次埃尔米特插值具有保形性;而3次样条插值要求其二阶导数也连续,所以插值函数的性态更好。

interp2( ): 二维插值函数

调用格式: Z1=interp2(X,Y,Z,X1,Y1,method)

其中，X、Y是两个向量，表示两个参数的采样点,Z是采样点对应的函数值。X1、YI是两个标量或向量，表示要插值的点。

数据插值能够根据已知数据推算未知数据，这使得人们解决问题的能力得到了拓展和延伸。

曲线拟合(plotfit)

插值要求逼近函数在采样点的数值与原函数相等，然而在实验中，测量的数据不一定准确，如果强求逼近函数过样本点，显然是不合理的。使用曲线拟合可以避免这种情况。

曲线拟合的原理

曲线拟合的实现方法

polyfit( ):多项式拟合函数 函数功能:求得最小二乘拟合多项式系数。

调用格式:

P=polyfit(X,Y,m)
[P,S]=polyfit(X,Y,m)
[P,S,mu]=polyfit(X,Y,m)

根据样本数据X和Y，产生一个m次多项式P及其在采样点误差数据S，mu是一个二元向量，mu(l)是mean(X),而mu(2)是std(X)。

二维曲线

plot函数：

(1)plot函数的基本用法: plot(x,y)其中，x和y分别用于存储x坐标和y坐标数据。

%例一 绘制一条折线
x=[2.5,3.5,4,5];
y=[1.5,1,1.5];
plot(x,y)

(2)最简单的plot函数的调用格式： plot(x) 图形的横坐标，是x元素的索引。

y=[1.5,1,1.5];
plot(x)

当plot函数的参数x是复数向量时，则分别以该向量元素实部和虚部为横,纵坐标4绘制出一条曲线。

(3)plot(x,y)函数参数的变化形式

当x是向量，y是矩阵时

如果矩阵y的列数等于x的长度，则以向量x为横坐标，以y的每个行向量为纵坐标绘制曲线，曲线的条数等于y的行数
如果矩阵y的行数等于x的长度，则以向量x为横坐标，以y的每个列向量为纵坐标绘制曲线，曲线的条数等于y的列数。

当x、y是同型矩阵时

以x、y对应列元素为横、纵坐标分别绘制曲线，曲线条数等于矩阵的列数

(4)含多个输入参数plot函数plot(x1,y1,x2,y2,…,xn,yn)

其中，每一个向量对构成一组数据点的横、纵坐标，绘制一条曲线。

(5)含选项的plot函数 plot(x,y,选项)

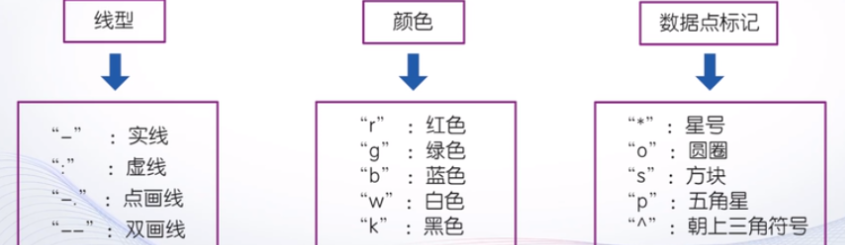
fplot函数：

x往往采取等间隔采样，如果在函数随着自变量的变化未知或者在不同区间的函数频率特性差别大，如果采用plot函数时自变量的采样间隔设置不合理，则无法反映函数的变化趋势。

如何解决这个问题呢？——fplot可根据参数函数的变化特性，自适应地设置采样间隔。

(1)fplot函数的基本用法： fplot(f,lims,选项)

其中，f代表一个函数，通常采用函数句柄的形式。lims为x轴的取值范围，用二元向量[xmin,xmax]描述，默认值为[-5,5]。选项定义与plot函数相同。

(2）双输入函数参数的用法 fplot(funx, funy, tlims,选项)
其中，funx、funy代表函数，通常采用函数句柄的形式。tlims为参数函数funx和funy的自变量的取值范围，用二元向量[tmin，tmax]描述。

绘制图形的辅助操作

给图形添加标注

title函数
- title函数的基本用法： title(图形标题)
- 在图形标题中使用Latex格式控制符： \bf 加粗 \it 斜体 \rm 整体
- 含属性设置的title函数 title(图形标题,属性名,属性值)
  
  Color属性：用于设置图形标题文本的颜色。
  
  FontSize属性：用于设置标题文字的字号。
xlabel函数和ylabel函数 xlabel(x轴说明) ylable(y轴说明)
text函数和gtext函数：

text(x,y,说明) gtext(说明)

gtext函数没有坐标参数，执行命令时，十字光标跟随鼠标移动，单击鼠标，即可将说明放置在十字光标处。
legend函数 legend(图例1,图例2,…)

坐标控制

axis函数
- axis([xmin,xmax,ymin,ymax,zmin,zmax])
- axis的其他用法：
  
  axis equal: 纵、横坐标采用等长刻度 axis square: 产生正方形坐标系(默认为矩形)
  
  axis auto: 使用默认设置 axis off：取消坐标轴 axis on：显示坐标轴
  
  axis equal后，如：x轴0到1长度等于y轴0到1长度。消除因为x轴和y轴刻度长不等带来的图像变形。
给坐标系加网格和边框(grid)

grid on:控制显示网格线 grid off:控制不显示网格线 grid:在两种状态之间进行切换

box函数 box on,box off,box。用法同grid。

图形保持(hold)

在已经存在的图形叠加图形

hold on   % 控制保持原有图形
hold off  % 控制刷新图形窗口
hold      % 两种模式间切换

d 图形窗口的分割(subplot)

子图：同一图形窗口中的不同坐标系下的图形称为子图。

subplot函数： subplot(m,n,p) 其中，m,n指定将图形窗口分成m * n个绘图区，p指定当前活动区。

x=linspace(0,2*pi,60):
subplot(2,2,1) %将整个坐标图分成两行两列，按行数的第一个子图
plot(x,sin(x)-1);
title('sin(x)-1');axis([0,2*pi,-2,0])
subplot(2,1,2) %将整个坐标图分成两行1列，按行数的第2个子图
plot(x,cos(x)+1);
title('cos(x)+1');axis([0,2*pi,0,2])
subplot(4,4,3) %将整个坐标图分成4行4列，按行数的第3个子图
plot(x,tan(x));
title('tan(x)');axis([0,2*pi,-40,40])
subplot(4,4,8) %将整个坐标图分成4行4列，按行数的第8个子图
plot(x,cot(x));
title('cot(x)');axis([0,2*pi,-35,35])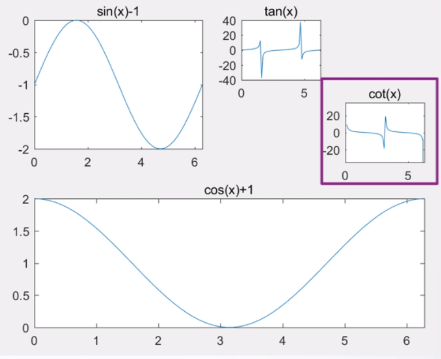

其他形式的二维图形

其他坐标系下的二维曲线图

对数坐标图(semilogx;semilogy;loglog)

semilogx: x使用常用对数刻度,y为线性刻度

semilogy: y使用常用对数刻度,x为线性刻度

loglog:x,y都使用常用对数刻度

极坐标图(polar)

polar(theta,rho,选项) %其中,theta为极角，rho为极径，选项的内容与plot函数相同。

统计图

条形类图形（bar、barh；hist、rose）

条形图：

bar函数: 竖直条形图，bar(y,style)其中y是数据,选项style用于指定分组排列模式。grouped簇状分组，stacked堆积分组。 bar(x,y,style)其中，x存储横坐标，y存储数据

barh函数:水平条形图使用方式与bar函数类型

直方图：

hist函数:直角坐标系

hist(y)，hist(y,x)其中，参数y是要统计的数据，x用于指定区间的划分方式。

x:用于设置统计区间的划分方式，若统计数据为标量，则统计数据均分为x个小区间，若x是向量，则x中的每一个数指定分组的中心值，元素的个数为数据分组数，x缺省时，默认按10个等分区间进行统计。

rose函数:极坐标系

rose(theta,x) 其中，参数theta用于确定每一区间与原点的角度，选项x用于指定区间的划分方式。

theta:是一个向量，绘图时将圆划分为若干个角度相等的扇形区域，每个扇形高度为落入这个扇形区域的theta个数。如果x是标量，则将0到2pi划分为x个扇形区域，默认20。
```
%  绘制高斯分布数据在极坐标下的直方图。
y=randn(500,1);
theta=y*pi;
rose(theta)
title("在极坐标下的直方图")
```
面积类图形（pie;area）
- 1扇形图 pie函数 pie(x,explode)
  
  其中，参数x存储待统计数据，选项explode控制图块的显示模式
- 2面积图 area函数 area(x, y)：
  
  该函数以参数x和y绘制面积图。如果x和y为向量，则相当于函数plot(x, y)，并将0到y之间进行了填充。如果参数y为矩阵，则将y的每一列绘制面积图并进行叠加。
散点类图形（scatter;stairs;stem）
- scatter函数：散点图
  
  scatter(x,y,选项,‘filled’)参数x,y用于定位数据点，选项用于指定线型，颜色，数据点标记。
  
  filed:填充数据点标记
- stairs函数：阶梯图
- stem函数：杆图

矢量图形(compass;feather;quiver)

compass：
compass(x,y)：x,y是n维向量，显示n个箭头，箭头的起点为原点，箭头位置为（x(i),y(i)）.
compazz(z):参量z为n维复数向量，命令显示n个箭头，箭头起点为原点，箭头位置为（real(z),image(z)）。
feather：
feather(x,y) :函数绘制由向量参量x与y构成的速度向量，沿水平轴方向，从均匀间隔点以箭头发射出来
feather(z) :函数绘制羽毛图。参量z是一个复数，则feather(z)相当于compass(real(z)，imag(z))；
quiver函数调用格式:

quiver(x, y, u, v)其中，(x, y)指定矢量起点，(u, v)指定矢量终点。

三维曲线

plot3函数

(1)plot3函数的基本用法：plot3(x,y,z)其中，参数x、y、z组成一组曲线的坐标。

(2)含多组输入参数的plot3函数： plot3(x1,y1,z1,x2,y2,z2,…,xn,yn,zn)

每一组x,y,z向量构成一组数据点的坐标，绘制一条曲线

(3)含选项的plot3函数：选项用于指定曲线的线型，颜色和数据点标记。

fplot3函数

fplot3(funx,funy,funz,tlims)

其中,funx、funy、funz代表定义曲线x、y、z坐标的函数，通常采用函数句柄的形式。tlims为参数函数自变量的取值范围，用二元向量[tmin，tmax]描述﹐默认为[-5，5]。

三维曲面

平面网格数据的生成

(1)利用矩阵运算生成

(2)利用meshgrid函数生成，[X,Y]=meshgrid(x,y)；其中，参数x、y为向量，存储网格的X，Y为矩阵

绘制三维曲面的mesh函数和surf函数

基本调用格式

mesh(x,y,z,c)
surf(x,y,z,c)

其中x、y是网络坐标矩阵，z是网格点上的该网格点上的高度矩阵，c用于指定在不同高度下的曲面颜色。

其他调用格式: mesh(z,c) surf(z,c)

当x,y省略时，z矩阵的第2维下标当作x轴坐标，z矩阵的第1维下标当作y轴坐标。

带等高线的三维网格曲面函数meshc
带底座的三维网格曲面函数meshz
具有等高线的曲面函数surfc
具有光照效果的曲面函数surfl

标准三维曲面（sphere;cylinder；peaks）

(1) sphere函数 [x,y,z]=sphere(n)

(2)cylinder函数 [x,y,z]=cylinder(R,n)

面和柱面。
sphere将产生3个n+1阶的方阵，可以绘制出圆心位于原点，半径为1的单位球体，如果调用该函数时，不带输出参数，则直接绘制球面，n决定球面圆滑程度，默认20，n越大，越光滑。
cyinder函数的R是一个向量，存放柱面各个等间隔高度上的半径，n表示在圆柱圆周上有n个间隔点，默认20个，n越大，越滑。如果R是一个标量，则生成一个圆柱面。

(3)peaks函数